Laboratoriniai darbai
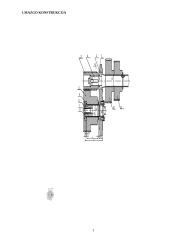
Strypinių konstrukcijų skaičiavimas baigtinių elementų metodu
0
1,25EI
1,5EI
1,0EI
Naikiname konsoles:
0,75 kN/m
4,80 kN
4,80 kN
4,32 kNm
6,
0
5,4
2,
0
2,
0
Rodome globalinius konstrukcijos poslinkius:
U3
U4
U2
U1
Sudarome diskretinį modelį baigtiniais elementais:
U1,1
U1,3
U1,2
U1,4
6,
0m1,25EI
U2,1
U2,2
U2,3
U2,4
5,40m
1,5EI
U3,3
U3,4
U3,1
U3,2
4,
0m1,0EI
Kiekvienam elementui skaičiuojame standumo matricą kK :
−
−−−
−
−
=
22
22
3
233
3636
323
3636
2
LLLL
LL
LLLL
LL
L
EI
K k
Standumo matrica pirmojo elemento:
−
−−−
−
−
=
83333,020844,041667,020844,0
20844,006944,020844,006944,0
41667,020844,083333,020844,0
20844,006944,020844,006944,0
*1 EIK
Standumo matrica antrojo elemento:
−
−−−
−
−
=
11111,130864,055556,030864,0
30864,011431,030864,011431,0
55556,030864,011111,130864,0
30864,011431,030864,011431,0
*2 EIK
Standumo matrica trečiojo elemento:
−
−−−
−
−
=
0,13750,050,03750,0
3750,01875,03750,01875,0
50,03750,00,13750,0
3750,01875,03750,01875,0
*3 EIK
Sudarome diagonalinę matrica K :
−
−−−
−
−
−
−−−
−
−
−
−−−
−
−
⋅=
0,13750,050,03750,0
3750,01875,03750,01875,0
50,03750,00,13750,0
3750,01875,03750,01875,0
11111,130864,055556,030864,0
30864,011431,030864,011431,0
55556,030864,011111,130864,0
30864,011431,030864,011431,0
83333,020844,041667,020844,0
20844,006944,020844,006944,0
41667,020844,083333,020844,0
20844,006944,020844,006944,0
EIK
Užsirašome pagrindine poslinkių metodo lygtį:
[ ] [ ] [ ] { } { }FuCKC T
=⋅⋅⋅
[ ]K - diagonalin÷ matrica;
{ }F - mazginių išoenių apkrovų vektorius. { }F turi tiek komponenetų, kiek
globalinis poslinkis komponentų;
[ ]C - poslinkių darnos matrica. Ji susieja elementų poslinkius { }u su
globaliniais poslinkiais { } { }uCu ⋅=
Sudarome poslinkių darnos matricą [ ]C :
⋅
=
4
3
2
1
4,3
3,3
2,3
1,3
4,2
3,2
2,2
1,2
4,1
3,1
2,1
1,1
1
1
1
1
1
1
U
U
U
U
U
U
U
U
U
U
U
U
U
U
U
U
Sudarome tansponuotają poslinkių darnos matricą [ ]TC :
[ ]
=
1
1
11
11
TC
Dabar [ ]TC dauginame iš K :
[ ]
−
−
−−
−−−−
⋅=⋅
0,1375,05,0375,0
55555,030864,011111,130864,0
11111,130864,055555,030864,041667,020833,08333,020833,0
375,01875,0375,01875,020833,006944,020833,006944,0
EIKC T
Darbar galutinai sudarome globalinę standumo matricą [ ]K = [ ] [ ]CKC T
⋅⋅
[ ]
−
−
⋅=
0,13750,0
11111.155556.0
55556.094444.120833,0
3750,020833,025694,0
EIK
Iššorin÷s apkrovos F nustaymas:
Iššorin÷ apkrova susideda iš mazginių j÷gų 0F ir į mazgus suvestų mazginių apkrovų pF .
pFFF += 0 ;
=
0
0
0
80.4
0F
FCF T
p ⋅=
pkF , reikšmes nustatome kiekvienam r÷mo elementui.
F1,1
P1,3
F1,2
F1,4
6,
0m
0,75 kN/m
−
=
⋅
−
⋅⋅
⋅
⋅⋅
=
⋅
−
⋅⋅
⋅
⋅⋅
=
=
25,2
25,2
25,2
25,2
12
0,675,0
0,675,0
2
1
12
0,675,0
0,675,0
2
1
12
2
1
12
2
1
2
2
2
2
4,1
3,1
2,1
1,1
,1
Lp
Lp
Lp
Lp
F
F
F
F
F p
=
=
0
0
0
0
4,2
3,2
2,2
1,2
,2
F
F
F
F
F p
F3,3
F3,4
4,
0m
F3,1
F3,2
4,32kNm
−
−
−
=
⋅
⋅−
⋅
⋅⋅
⋅
⋅−
⋅
⋅⋅
−
=
⋅
−
⋅
⋅⋅
⋅
−
⋅
⋅⋅
−
=
=
08,1
62,1
08,1
62,1
32,4
4
)222(2
32,4
4
226
32,4
4
)222(2
32,4
4
226
)2(
6
)2(
6
2
3
2
3
2
3
2
3
4,3
3,3
2,3
1,3
,3
M
L
baa
M
L
ba
M
L
abb
M
L
ba
F
F
F
F
F p
Tur÷dami visas pkF , reikšmes pradedame konstruoti F :
−
−
−
−
=
=
08,1
62,1
08,1
62,1
0
0
0
0
25,2
25,2
25,2
25,2
4,3
3,3
2,3
1,3
4,2
3,2
2,2
1,2
4,1
3,1
2,1
1,1
F
F
F
F
F
F
F
F
F
F
F
F
F
Tur÷dami F galime apskaičiuoti pF pagal formulę:
FCF T
p ⋅=
−
=
−
−
−
−
⋅
=
08,1
0
25,2
87,3
08,1
62,1
08,1
62,1
0
0
0
0
25,2
25,2
25,2
25,2
1
1
11
11
pF
Galutinai suskaičiuoju F:
−
=
−
+
=+=
08,1
0
25,2
67,8
08,1
0
25,2
87,3
0
0
0
80,4
0 pFFF
Dabar sugrįžtam prie pusiausvyros lygties [ ] { } [ ]FuK =⋅ :
−
=
⋅
−
−
⋅
08,1
0
25,2
67,8
0,13750,0
11111,155556,0
55556,094444,120844,0
3750,020844,025694,0
4
3
2
1
u
u
u
u
EI
Suskaičiavę gauname globalinius poslinkius:
EI
u
EI
u
EI
u
EI
u
094,32
857,4
714,9
464,88
4
3
2
1
=
=
−
=
=
Darome grįžtamąjį ryšį prie formul÷s { } { }uCu ⋅= ir įstatom globalinius poslinkius:
EI
EI
EI
EI
EI
U
U
U
U
U
U
U
U
U
U
U
U
1
094,32
464,88
0
0
714,9
0
857,4
0
0
0
714,9
4649,88
094,32
857,4
714,9
464,88
1
1
1
1
1
1
4,3
3,3
2,3
1,3
4,2
3,2
2,2
1,2
4,1
3,1
2,1
1,1
⋅
−
−
=
−
⋅
=
Nustatau kiekvienam elementui mazgų poslinkius:
EI
u
1
0
0
714,9
464,88
1 ⋅
−
= ;
EI
u
1
714,9
0
857,4
0
2 ⋅
−
= ;
EI
u
1
094,32
464,88
0
0
3 ⋅
=
Kai turime atskirų elementų mazgų poslinkius galima sudaryti įražų diagramas. Kiekvienam
baigtiniam elementui tokia forma: kpkkk FuKP −⋅=
−
=
−
−⋅
−
⋅
−
−−−
−
−
⋅=
642,16
368,6
095,8
868,1
25,2
25,2
25,2
25,2
1
0
0
714,9
464,88
83333,020844,041667,020844,0
20844,006944,020844,006944,0
41667,020844,083333,020844,0
20844,006944,020844,006944,0
1 EI
EIP
−
−
=
−⋅
−
⋅
−
−−−
−
−
⋅=
095,8
499,1
0
499,1
0
0
0
0
1
714,9
0
857,4
0
11111,130864,055556,030864,0
30864,011431,030864,011431,0
55556,030864,011111,130864,0
30864,011431,030864,011431,0
2 EI
EIP
−
−
=
−
−
−
−⋅
⋅
−
−−−
−
−
⋅=
0
932,2
047,16
932,2
08,1
62,1
08,1
62,1
1
094,32
464,88
0
0
0,13750,050,03750,0
3750,01875,03750,01875,0
50,03750,00,13750,0
3750,01875,03750,01875,0
3 EI
EIP
Prieiname prie pirmojo elemento įražų:
−
−
+
−
=
−
−
=
=
642,16
368,6
095,8
868,1
4,1
3,1
2,1
1,1
2,1
2,1
1,1
1,1
1
P
P
P
P
M
V
M
V
S
Antrojo:
+
+
+
=
−
−
=
=
095,8
499,1
0
499,1
4,2
3,2
2,2
1,2
2,2
2,2
1,2
1,2
2
P
P
P
P
M
V
M
V
S
Trečiojo:
+
−
+
=
−
−
=
=
0
932,2
047,16
932,2
4,3
3,3
2,3
1,3
2,3
2,3
1,3
1,3
3
P
P
P
P
M
V
M
V
S
Braižome lenkimo momentų ir skersinių j÷gų diagramas:
4,32
16
,0
47
10
,1
84
5,
86
4 8,
09
5
16
,6
42
8,095
M
-
6,
36
8
1,
86
8
+
1,4991,499
2,
93
2
2,
93
2
4,80
+
+
V
Braižome ašinių j÷gų diagramą:
1,
49
9
1,
49
9
-
+
-
-
-
1,868
4,80
1,
49
9
3,
30
1
1,868
N
Kai turime diagramas nustatome atramines reakcijas:
N
V
MR
2,932
3,301
16,047
MR
N
V
6,368
1,499
16,642
.301,3
932,2
047,16
kNN
kNV
kNmM R
=
=
=
.499,1
368,6
642,16
kNN
kNV
kNmM R
=
=
=
TIKRINU SKAIČIAVIMUS:
=
=
=
∑
∑
∑
0
0
0
K
Y
X
M
F
F
=⋅⋅−
−+⋅+⋅++⋅+⋅−
=+−−
=+⋅+−−
03675,0
642,164,5499,16368,6047,169,0301,34932,2
080,4499,1301,3
080,4675,0368,6932,2
=−
=−
=−
0280,54225,54
080,480,4
030,930,9
≈−
=
=
003,0
00
00
0,75 kN/m
4,80 kN
4,80 kN
N=3,301kN
V=2,932kN
MR=16,047kNm
MR=16,642kNm
N=1,499kN
V=6,368kN
K
6,
0
2,
0
2,
0
5,40,9
1. Nustatyti lenkiamo ir tempiamo ar gniuždomo strypinio elemento standumo
matricos dviejų koeficientų bendrąsias išraiškas
a) Tempiamas – gniuždomas elementas
Uk,1 Uk,2
Lk
y
x
Užsiduodame poslinkių kitimą Ox ašies kriptimi d÷snį:
xaaxU kx 21)( +=
Randame koeficientus a1 ir a2 iš kraštutinių sąlygų:
1) Kai x=0, tai uk1=a1;
2) Kai x=lk, tai uk2=a1+a2lk;
Darbar išsireiškiame a1 ir a2:
a1=uk1;
a2=(uk2-uk1)/lk;
gautus...
Šį darbą sudaro 4252 žodžiai, tikrai rasi tai, ko ieškai!
★ Klientai rekomenduoja
Šį rašto darbą rekomenduoja mūsų klientai. Ką tai reiškia?
Mūsų svetainėje pateikiama dešimtys tūkstančių skirtingų rašto darbų, kuriuos įkėlė daugybė moksleivių ir studentų su skirtingais gabumais. Būtent šis rašto darbas yra patikrintas specialistų ir rekomenduojamas kitų klientų, kurie po atsisiuntimo įvertino šį mokslo darbą teigiamai. Todėl galite būti tikri, kad šis pasirinkimas geriausias!
Norint atsisiųsti šį darbą spausk ☞ Peržiūrėti darbą mygtuką!
- Mechanikos laboratorinis darbas
- 17 psl., (4252 ž.)
- PDF dokumentas 269 KB
- Lygis: Universitetinis
Mūsų mokslo darbų bazėje yra daugybė įvairių mokslo darbų, todėl tikrai atrasi sau tinkamą!
Panašūs darbai
Privalumai
Atsisiuntei rašto darbą ir neradai jame reikalingos informacijos? Pakeisime jį kitu nemokamai.
Pirkdamas daugiau nei vieną darbą, nuo sekančių darbų gausi 25% nuolaidą.
Išsirink norimus rašto darbus ir gauk juos akimirksniu po sėkmingo apmokėjimo!
Atsiliepimai