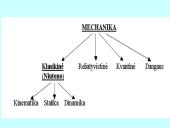
Šperos
Kinematika. Statika
Kinematika 1.Vektorinis taško apibrėžimo būdas patogus teoremose , skaičiavimuose, nes vietoj trijų funkcijų x=x(t), y=y(t), z=z(t), turime tiktai vieną Turėdami koordinatinį taško judėjimo apibrėžimą, galima jį pakeisti vektoriniu r=xi+yj+zk x,y,z- taško koordinatės I,j,k koordinačių ašių aortai, Visos šios laiko momento t funkcijos išreiškiančios taško judėjimą yra viena reikšmės tolydinės ir diferencijuojamos t atžvilgiu 4. Kai judėjimas yra greitėjantis tada greičio ir tangentinio pagreičio kryptys yra vienodos Jeigu taškas juda lėtėdamas tada greičio ir tang, pagr,kryptys yra priešingos 5. Nagrinėjant slenkamąjį judėjimą kinematikoje užtenka ištirti to kūno vieno vieno taško judėjimą Kūno kaip ir taško padėtis apibrėžiama trimis koordinatėmis pav, Dekarto koordinatėmis, 7. Kampinis pagreitis Ši formulė taikoma tada,kai žinoma kampinio greičio priklausomybė nuo posūkio kampo Kamp gr rad\s kampinis pagreitis rad\s2 Jeigu kūnas sukasi prieš laikrodžio rodyklę laikoma kad kamp greitis yra teigiamas priešingu atveju – neigiamas Kai > 0 ir > 0 sukimasis greitėjantis , kai > 0 ir 0 - sukimasis lėtėjantis, 3. Taško pagreitis ir projekcijos Dekarto ašyse Vidutinis pagreitis per laiko pokytį t lygus Taško pagreitis tam tikru laiko momentu yra pirmoji greičio išvestinė arba antroji padėties vektoriaus išvestinė laiko atžvilgiu Taško pagreičio projekcija kurioje nors ašyje lygi greičio projekcijos toje ašyje išvestinei arba judančio taško koordinatės antrąjai išvestinei laiko atžvilgiu Žinodami pagr projekcijas galim apskaičiuoti kampus tarp koordinačių ašių ir pagreičio vektoriaus a, Pagal šias formules galim sudaryti tapatybę pagal kurią tikriname ar teisingai apsk pagreičio kryptis 9. Reliatyv. keliamasis ir absoliut. Judėjimai. Taško judėjimas nejudančios koordinačių sistemos atžvilgiu vad absoliučiu o judančios sistemos atžvilgiu reliatyviuoju Keliamuoju judėjimu vad judančios koord sistemos ir visų nekintamai su ja susijusių taškų judėjimas Absoliučiąja taško trajektorija vad kreivė kurią brėžia taškas nejudančios koord sistemos atžvigiu Keliamoji trajektorija kiekvienu laiko momentu yra kitokia Reliatyviuoju keliamuoju arba absoliučiuoju taško greičiu ir pagreičiu vad jo greitis ir pagreitis atitinkamame judėjime Visų šių judėjimų trajektorijos greičiai ir pagreičiai yra skirtingi 10. Greičių sudėties teorema. Taško vektorius sieja lygybė r1=r0+r Absoliutus taško greitis v lygus padėties vektoriaus r1 išvestinei laiko atžvilgiu Surašę reikšmes į 1 lygtį gauname Vektorių v0 ir suma yra taško keliamasis greitis Vadinasi taško kurio judėjimas sudėtinis ,absoliutus greitis lygus keliamojo ir reliatyv greičių geometrinei sumai 11 Koriolio teorema Absoliutusis taško pagreitis lygus keliamojo reliatyviojo ir Koriolio pagreičių geometrinei sumai a = ak + ar + ac. ac -Koriolio pagreitis - kampas tarp reliatyviojo greičio ir kampinio greičio Koriolio pagreitis statmenas abiem vektoriams ir vr 12. Kūno plokščiojo jud dėsnis Plokščiuoju vad. toks kūno judėj., kai judančio kūno bet kurio taško atstumas nuo tam tikros nejudamos plokštumos visą laiką yra pastovus Plokščio jud pavyzdys rato riedėjimas tiesiu keliu Teorema bet kurį figūros judėjimą jos plokštumoje galima išskaidyti į slinkimą ir sukimąsi apie laisvai pasirinktą polių Visi figūros taškai apie polių sukasi tuo pačiu kampiniu greičiu kampiniai pagreičiai vienodi 13. Plokščiai jud kūno t greič skaič poliaus metodu Slenkamajame judėjime visų kūno taškų greičiai yra vienodi todėl kūno bet kurio taško keliamasis greitis lygus poliaus greičiui o reliatyvusis sukimosi apie polių greičiui Va=Vb+Vab Vb – poliaus greitis Vab – greitis kuriuo taškas sukasi apie polių Teorema Dviejų figūros taškų greičių projekcijos tiesėje jungiančioje tuos taškus yra lygios Pagal šią formulę galima apskaičiuoti vieno figūros taško greitį kai žinomas kito taško greitis ir sukimosi kampinis greitis 14. Plokšč jud kūno greič sk projekcijų teorema Dviejų kūno taškų greičių vektorių projekcijos į tiesę jungiančią tuos taškus yra lygios viena kitai Pasinaudojus šiuo rezultatu galima lengvai rasti bet kurio taško greitį jei žinoma jo kryptis ir kurio nors taško priklausančio tam pačiam kūnui greitis didumas ir kryptis. 15. Greičių skaičiavimas taikant gr. centrą. Momentiniu greičių centru vadin tas kūno taškas kurio greitis tuo laiko momentu yra lygus nuliui Jei kūnas neslenka tai kiekvienu laiko momentu t toks taškas tikrai yra Kūno bet kurio taško greitis lygus greičiui gautam sukantis kūnui apie momentinį greičių centrą Cv. . vA vB iš čia galime daryti išvadą kad kūno taškų greičiai proporcingi tų taškų atstumams nuo momentinio greičių centro Va /CvA=Vb/ CvB 16. Pagreičių skaič taikant poliaus metodą. Ploščiai judančio kūno taško pagreitį galima apskaičiuoti pagal analogišką greičio formulę aA=aB+aAB aA – taško A pagreitis aB –taško B pagreitis aAB – pagreitis kuriuo taškas A sukasi apie tašką B Kadangi keliamasis judėjimas yra judėjimas kūnui slenkant tai jo Koriolio pagreitis lygus nuliui Pagreitį aAB galime išskaidyti į normatinį ir tangentinį komponentus aAB= aABn+aABt Statika. 12 Slydimo trintis. Liečiantis dviems kūnams atsiranda trinties jėga kuri trikdo vienam kūnui slysti kitu kūnu Trinties jėga visada veikia priešinga kryptimi negu jėga kuri stengiasi pastumti kūną 1. didžiausia Ftr nepriklauso nuo to kokio didumo plotu liečiasi kūnai 2. Didžiausia Ftr tiesei proporcinga spaudžiančios kūnus vieną prie kito normalinės jėgos N didumui 3. Didžiausia Ftr priklauso nuo susiglaudusių kūnų medžiagos ir jų paviršių glotnumo . Trinties jėgos kryptis visada priešinga greičio krypčiai ir jos modulis apskaiciuojamas : Trinties koeficientas atitinkantis didžiausią trinties jėgą vad statinės trinties koeficientu Trinties koeficientas apsk pagal slystantį kūną veikiančią jėgą vad kinetines tirnties koeficientu Riedėjimo trintis . Ratas pradeda judėti horizontaliu keliu kai jį traukianti horizontali jėga P pasidaro didesnė už tam tikrą kritinę jėgą Pkr Jei P mažiau arba lygu Pkr ratas nerieda Jei P daugiau už Pkr – rieda r-rato spindulys N – normalinės reakcijos jėga k-riedėjimo trinties koeficientas, jo matavimo vienetai metrai Ried trint koef nustatomas atliekant bandymus jis priklauso nuo medžiagų iš kurių yra pagaminti besiliečiantys kūnai, ir nuo kai kurių kitų veiksnių 13. Kūnų sistemos pusiausvyra Kūnų sistema tai visuma tokių kūnų kurių judėjimas ir pusiausvyra tarpusavy priklausomi Vidiniai ryšiai jungia kūnus į sistemą, išoriniai ryšiai tai ryšiai kai kūnų sistema pritvirtinama prie atramų ar kitų kūnų Kūnų sistemos pusiausvyra tiriama remiantis akcijos – reakcijos akcioma: vidinės jėgos kuriomis kūnai veikia vienas kitą yar vienodo didumo ir krypties bet veikia priešingomis kryptimis Visų vidinių jėgų geometrinė suma ir momentų suma = 0 Jei nezinome nei reakciju moduliu,nei krypčiu tai jega skaidoma I komponentes pagal koordinačių ašis teigiamomis kryptimis Kūnu sistemos pusiausvyrą dar galima skaičiuoti ir pirma išskaidant sistemą į atskirus laisvus kūnus 14. Santvaros-tai standi konstrukcija sudaryta iš šarnyrais sujungtų tiesių strypų Taškai į kuriuos sueina strypų ašys vad mazgais Santvara vad plokščia jei visų jos strypų ašys yra pirmoje plokštumoje Sudaryta iš trijų strypų: AC BC AB Prijungę prie trik ABC du strypus gaunam vieną naują mazgą ( m-mazgų skaičius ) S=3+2(m-3)=3+2m-6=2m-3 Šią sąlygą būtina tenkinti kad santvara būtų standi ir statiškai išsprendžiama Jėga kuri veikia santvaros strypą vad įrėža Skaičiuojant santvaras daromos prielaidos: 1 visi strypai tiesūs 2 nėra trinties šarnyruose 3 visos išorinės jėgos santvarą veikia tik mazguose 4 nepaisoma strypų svorio Tokios santvaros strypai yra tik tempiami arba gniuždomi Santvaras skaičiuoti galima dviem būdais 1 mazgų išpjovimo metodu 2 Riterio metodu 15. Santvaros skaič mazgų išpjovimo būdu Pradedant skaič santvarą pirma nustatomos atramų reakcijos Išpjaunamas mazgas kuriame veikia ne daugiau kaip dvi nežinomos perpjautų strypų reakcijos Šio strypo reakcija žymima išilgai strypo ašies tolyn nuo mazgo Sudaromos dvi pusiausvyros lygtys gautai susikertančių jėgų sistemai Pagal apsk strypų reakcijas sprendžiame apie įražų pobūdį nes įražos ir reakcijos yra priešingų ženklų bet vienodo didumo Jeigu apskaičiuota įraža yra teigiamas skaičius tai jos kryptis buvo pasirinkta teisingai ir strypas yra tempiamas priešingu atveju strypas būtų gniuždomas 16 Santvaros skaičiavimas Riterio metodu Apskaičiuojame ryšių reakcijas Santvarą perpjauname į dvi dalis ne daugiau kaip per tris strypus kurių reakcijos nežinomos Vietoje perpjautų strypų braižome jų reakcijas (išilgai ašies tolyn nuo mazgo) Nagrinėjamos santvaros dalies būsena turi būti tokia pati kokia buvo priš perpjaunant santvarą Todėl prie tos nagrinėjamos dalies pridedamos jėgos kuriomis veikiama nagrinėjama dalis Sudarome tris pusiausvyros lygtis taip kad kiekvienoje lygtyje būtų tik viena nežinoma reakcija Paprastai tai būna momentų lygtys apie tris taškus kuriuose dvi nežinomos reakcjos susikerta veikimo tiesėmis ir lieka tik viena nežinoma Pagal apsk strypo reakciją darome išvadą apie strypo išvadą 17. Erdvinė susikertančių jėgų sistema ekvivalenti atstojamąjai R o pusiausvyros atveju R=0 ESJS-os atstojamoji projekcija bet kuriame taške lygi sudedamų jėgų projekcijos toje ašyje algebrinei sumai Žinodami atstojamosios jėgos projekcijas koordinačių ašyse galime apskaičiuoti atstojamosios jėgos didumą (modulį) Kampus alfa beta ir gamą apsk pagal formules Jeigu erd sus jėg sistema yra pusiausvyra tai atstojamoji lygi 0 R=0 ir visų jėgų projekcijos tose ašyse sumos lygios 0 Erd sus jėg sistemos pusiausvyrą galima išreikšti ir jų momentų lygtimis Šios lygtys yra pagrindinės sprendžiant uždavinius 18. Jėgos momento taško atžvilgiu vektorius Erdvinės sistemos jėgos suka kūną apie skirtingas ašis Jėgos momentą taško atžvilgiu patogu laikyti vektoriumi lygiu vektorių p ir r vektorinei sandaugai Vektorius Mo (p) statmenas r ir p plokštumai Jo kryptis tokia kad žiūrint iš vektoriaus galo į pradžią , vektorių r reikia pasukti kampu mažesniu už 180 laipsnių norint jį sutapdinti su vektorium p Vektoriaus Mo (p) modulis : Momento modulis lygus dvigubam trikampio plotui , kurio viršūnės momento centre ir jėgos pradžios ir galo taškuose , 19. Jėgų poros momento vektorius Poros poveikį standžiam kūnui apibūdina : 1 poros plokštuma 2 momento didumas 3 sukimosi kryptis Todėl porą galime vaizduoti vektoriumi vad momento vektoriumi Momento vektorius M yra statmuo poros PP plokštumai S Irtokios kryptie kad žiūrint iš galo į pradžią pora suktų kūną prieš laikrodžio rodyklę Momento vektoriaus modulis = poros momento didumui Porą galime perkelti iš vienos plokštumos į kitą jai lygiagrečią plokštumą ir kiloti toje pačioje plokštumoje iš vienos vietos į kitą todėl momento vektroius laikomas laisvuoju vektoriumi 20. Erdvinės porų sistemos pusiausvyra Tokią sistemą sudaro poros kurių plokštumos erdvėje įvairiai orientuotos Kiekvieną porą vaizduojame momento vektoriumi Šie vektoriai yra laisvieji tai porų sistema išreiškiama momentų vektoriais M1 M2 M3 ir t t Mn perkeltais į koordinačių pradžios tašką 0 Momentų vektorių sisitema ekvivalentiška vienam momento vektoriui vad porų sistemos suminiu momentu . Žinodami suminio momento projekcijas koordinačių ašyse apskaičiuojam didumą Krypties kampai alfa beta ir gama tarp suminių momentų ir koordinačių ašių lygūs Jeigu erdvinė porų sistema yra pusiausvyra tai suminis porų momentas =0 M=0 Ši lygtis būtina ir pakankama erdvinės porų sistemos pusiausvyrai 21. Jėgos momentai koordinačių ašių atžvilgiu . Norėdami apskaičiuoti jėgos P momentą taške A reikia jėgą B išskaidyti į komponentus P Py Pz Jėgos P momentas taško atžvilgiu lygus jos komponentų P Py Pz momentų to paties taško atžvilgiu sumai Jėgos momentas koordinačių ašies atžvilgiu = 0 jei jėga lygiagreti tai ašiai arba ją kerta Norint apskaičiuoti momentą apie ašį: vedame plokštumą statmeną ašiai ir projektuojame jėgą P į tą plokštumą ir po to plokštumoje skaičiuojame momentą apie tą tašką kuriame ašis kerta plokštumą 22. Erdvinės jėgų sistemos redukcija . Erdvinė Jėgų P1 P2 Pn sistema galime pakeisti jėga R ir pora kurios momentas M0 Toks pakeitimas vad redukcija O ši jėga vad erdvinės jėgų sistemos sumine jėga, poros momentas-suminiu momentu (0 – redukavimo centras) Suminės jėgos momentas apskaičiuojamas Kampai alfa beta ir gama esantys tarp suminės jėgos ir koord ašių apskaičiuojamos: Jėgos momentas taško 0 atžvilgiu = suminio momento projekcijai koord ašyse Suminio momento didumas: Jėgos projekcijos koord ašyse nepriklauso nuo jėgos veikimo taško padėties, o suminis momentas priklauso nuo redukcijos centro padėties 23. Erdvinės jėgų sistemos pusiausvyros sąlygos . Erd jėg sis pus atveju R=0 reiškia ir jos projekcijos ašyse =0 Erdv jėgų pusiaus sąlyg išreiškiamos ir momentų lygtimis Šios lygtys yra būtina ir pakankama erdvinės jėgų sistemos pusiausvyros sąlyga . 3.Plokščios susikertančios jėgų sistemos gemetrinė sudėtis . Susikertančios vadin tokios jėgos kurių veikimo tiesės kertasi vienme taške. Pvz. P1 , P2 , P3 . Geometriškai sudėję P1 ir P2 jėgas gauname jų atstojamąją R1 = P1 + P2 Paskui R1 geometriškai sudedame su jėga P3 ir gauname atstojamąją R . R = R1 + P3 R = P1 + P2 + P3 =
Šį darbą sudaro 1923 žodžiai, tikrai rasi tai, ko ieškai!
★ Klientai rekomenduoja
Šį rašto darbą rekomenduoja mūsų klientai. Ką tai reiškia?
Mūsų svetainėje pateikiama dešimtys tūkstančių skirtingų rašto darbų, kuriuos įkėlė daugybė moksleivių ir studentų su skirtingais gabumais. Būtent šis rašto darbas yra patikrintas specialistų ir rekomenduojamas kitų klientų, kurie po atsisiuntimo įvertino šį mokslo darbą teigiamai. Todėl galite būti tikri, kad šis pasirinkimas geriausias!
Norint atsisiųsti šį darbą spausk ☞ Peržiūrėti darbą mygtuką!
- Klasikinės mechanikos špera
- 5 psl., (1923 ž.)
- Word failas 284 KB
- Lygis: Mokyklinis
Mūsų mokslo darbų bazėje yra daugybė įvairių mokslo darbų, todėl tikrai atrasi sau tinkamą!
Panašūs darbai
Kiti darbai
Privalumai
Atsisiuntei rašto darbą ir neradai jame reikalingos informacijos? Pakeisime jį kitu nemokamai.
Pirkdamas daugiau nei vieną darbą, nuo sekančių darbų gausi 25% nuolaidą.
Išsirink norimus rašto darbus ir gauk juos akimirksniu po sėkmingo apmokėjimo!
Atsiliepimai